Implementing BatchNorm with Flax NNX

Goals

• Demonstrate NNX code to reimplement BatchNorm

Non-Goals

• Explain in detail what BatchNorm is and why it may be a good idea. I recommend DLAI as background reading.
• Explain the ResNet architecture. I find that the original paper is extremely well-written.

TL;DR what is BatchNorm?

Batch Norm is a fairly simple idea. Given a mini-batch $\mathcal{B}$ during training, and $x \in \mathcal{B}$, we compute

$$\mathrm{BN}(x) = \gamma \odot \frac{x - \mu_{\mathcal{B}}}{\sigma_{\mathcal{B}}} + \beta$$

where $\mu_{\mathcal{B}}$ and $\sigma_{\mathcal{B}}$ are the batch mean and standard deviation of the minibatch respectively, and $\gamma, \beta$ are learnable parameters.

We also keep a running standard deviation and average to use during test time.

Implementation

The Flax team recently launched a new NNX API to replace linen. One of the key benefits they claimed was that managing state is much easier the old Linen API. And I have to say that this holds up quite well. Much like pytorch, NNX makes use of stateful modules to represent neural networks.

Since you need to specify everything explicitly, this makes storing state (like if you want to implement BatchNorm!) really easy. Let's see how this looks in code:

class BatchNorm(nnx.Module):
    """Implementaiton of BatchNorm for ConvLayers only."""

    def __init__(self, n_features: int, eps: float = 1e-5, momentum: float = 0.9):
        normalization_shape = (1, 1, 1, n_features)

        # The scale parameter and the shift parameter (model parameters) are
        # initialized to 1 and 0, respectively
        self.gamma = nnx.Param(jnp.ones(normalization_shape))
        self.beta = nnx.Param(jnp.zeros(normalization_shape))

        # Init the moving mean to be one and variance to be zero
        self.moving_mean = nnx.BatchStat(jnp.zeros(normalization_shape))
        self.moving_var = nnx.BatchStat(jnp.ones(normalization_shape))

        self.eps = eps
        self.momentum = momentum

        # To make the module compatible with `.eval()`, need to define these parameters.
        self.use_running_average = False

    def __call__(self, x_bhwc: jax.Array) -> jax.Array:
        if self.use_running_average:
            x_hat_bhwc = (x_bhwc - self.moving_mean) / jnp.sqrt(
                self.moving_var + self.eps
            )
        else:
            # calculate in-batch mean and variance and use those values to normalize input
            in_batch_mean = jnp.mean(x_bhwc, axis=(0, 1, 2), keepdims=True)
            in_batch_var = jnp.var(x_bhwc, axis=(0, 1, 2), keepdims=True)

            x_hat_bhwc = (x_bhwc - in_batch_mean) / jnp.sqrt(in_batch_var + self.eps)

            self.moving_mean = (
                self.momentum * self.moving_mean + (1 - self.momentum) * in_batch_mean
            )
            self.moving_var = (
                self.momentum * self.moving_var + (1 - self.momentum) * in_batch_var
            )

        return self.gamma * x_hat_bhwc + self.beta

Some things to highlight:

• we use nnx.Param to store learnable parameters
• nnx.BatchStat is used to keep track of the running batch statistics (here it's mean and standard deviation). We could have used the base class nnx.Variable, but this is a handy subclass.
• During inference, we need to call .eval(). This will internally change self.use_running_average to be True.

Easy, right?

Experiments

To test that our BatchNorm actually works (and gives reasonable results), I implemented ResNet-50 and trained it on ImageNet.

After training for 45 epochs, I was able to get roughly 70% top 1 accuracy, and around 95% top 5 acccuracy when trained with a batch size of 256.

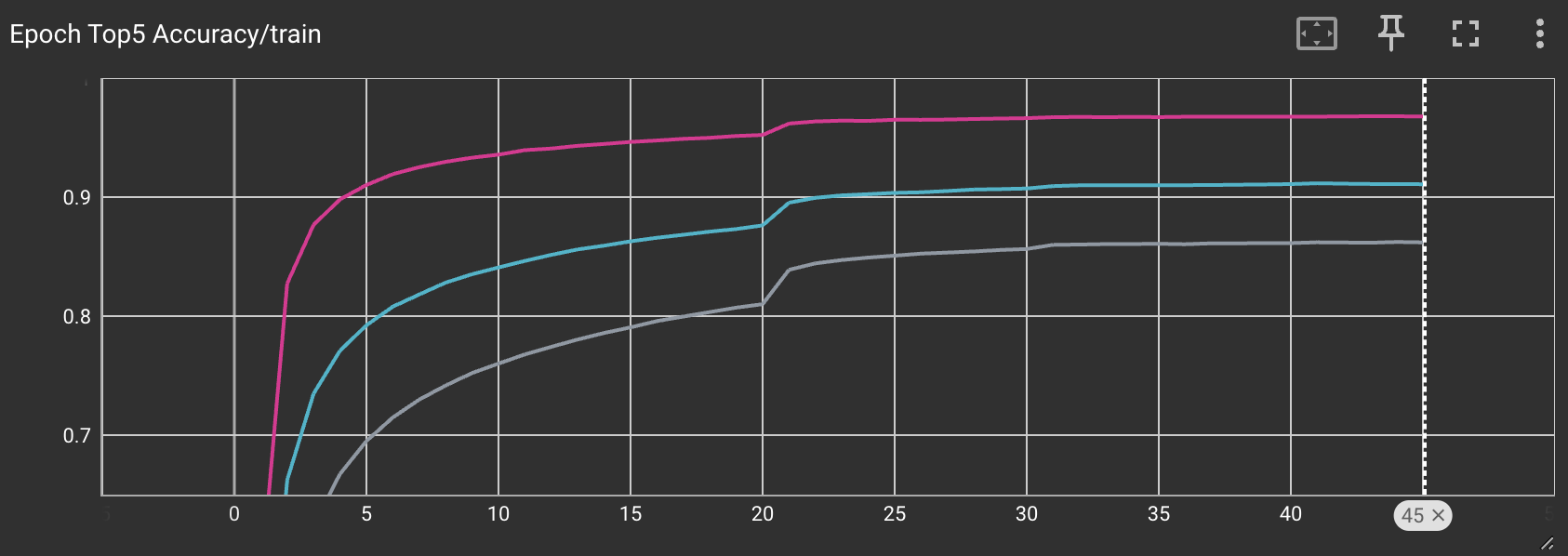
Here we see that varying the batch sizes can have a major effect on the final training accuracy. Unsurprisingly, using a larger batch size will yield better results since the normalization constants will be more accurate.

The code for training ResNet-50 (along with our implemenation of BatchNorm) can be found in this repo.

Acknowledgments

I'd like to thank TRC for providing some lovely TPUs free of charge.

If you have any comments or feedback for me, my twitter handle is @pushinproto.